Take a photo of a barcode or cover
When Livio does manage to address phi directly, he does so by debunking preexisting phi-myth. There are numerous instances of claims of phi related architecture, art, writing, and natural phenomenon, and Livio shows that many of these are not true, or at the very least, conjecture with no solid evidence. I wish that instead of spending so much time telling what phi is not and where it isn't found, Livio would have spent more time on instances where phi occurs. If I were to write a book about "glurbl," but spend the whole time telling you that cars aren't glurbl, neither are bowling balls, and despite popular belief, the Guggenheim museum is not a glurbl, by the end you would probably have no better idea of what glurbl is. That is what I felt about most of this book.
As the end of the book drew near, Livio managed to eke out a few examples of phi and better explain it's place in mathematics. Overall, however, I thought the book was better as a general overview of the history of mathematics and geometry, with the occasional contextual highlight on phi, than it was a comprehensive tome solely about phi. I was also disappointed that Livio proposed many theories, but he never really took a stand on the issues, instead leaving me with a vague impression that either could be right, and that he didn't care much which it was.
While not nearly the impressive book on phi that I had hoped for, Livio managed to present an interesting book on the general history of mathematics and geometry. I suppose that if you are interested in phi, then this is a good first read, as it will help you approach the other books with a more critical mind. Just don't expect this to be a book full of amazing phi occurrences and phenomenon.
The Golden Ratio is probably best explained in a diagram like this one:

The Golden Ratio can be used to construct a Golden Rectangle:
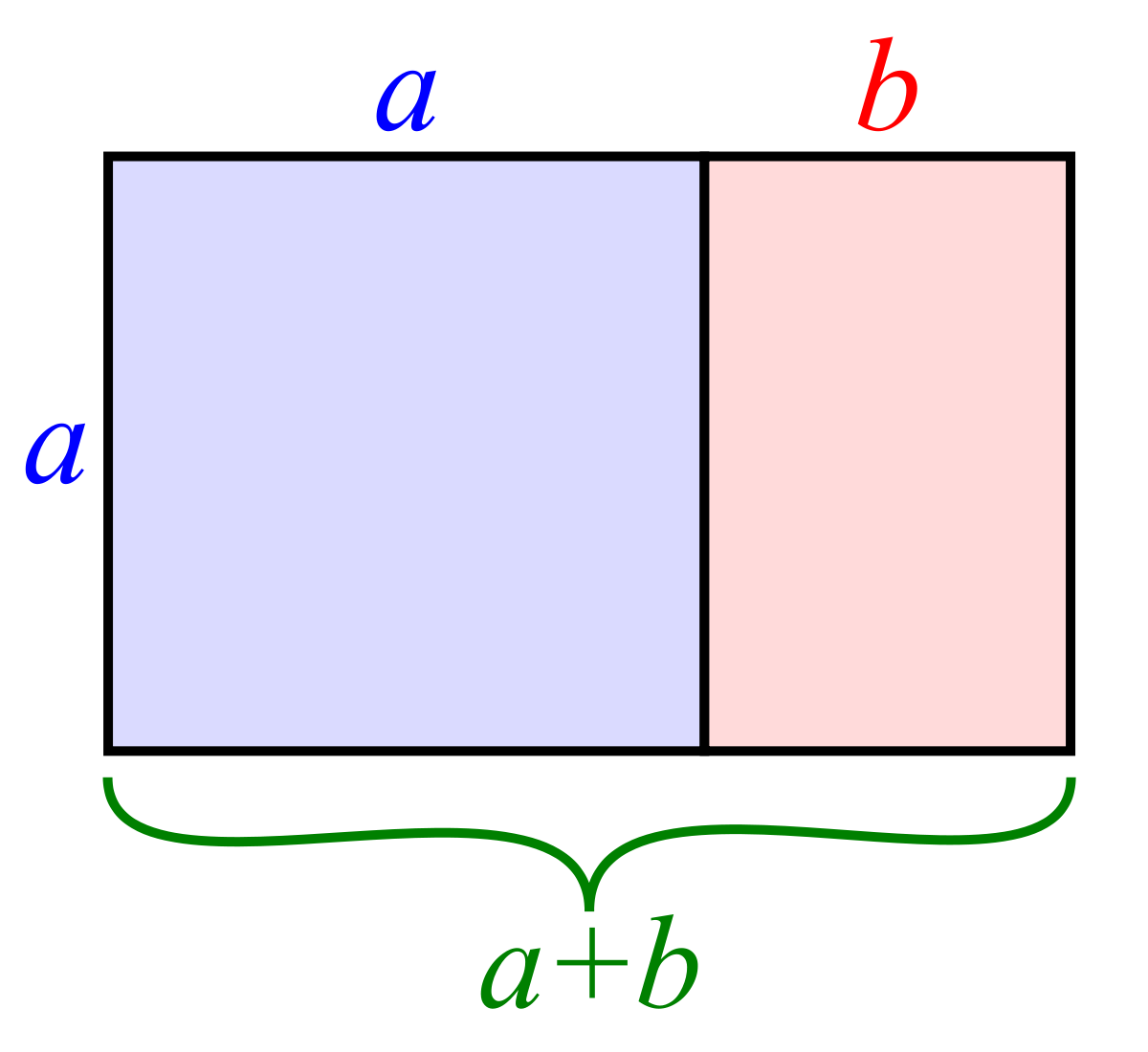
The pink rectangle that results from taking away the blue square is also a Golden Rectangle. If a square is subtracted from that rectangle, the remaining rectangle will also be a Golden Rectangle, and so on, ad infinitum:

Each daughter Golden Rectangle will be smaller than the parent Golden Rectangle by a factor of phi.
The Golden Spiral is a special kind of logarithmic spiral with a growth factor of phi. It can be approximated using a Fibonacci spiral:
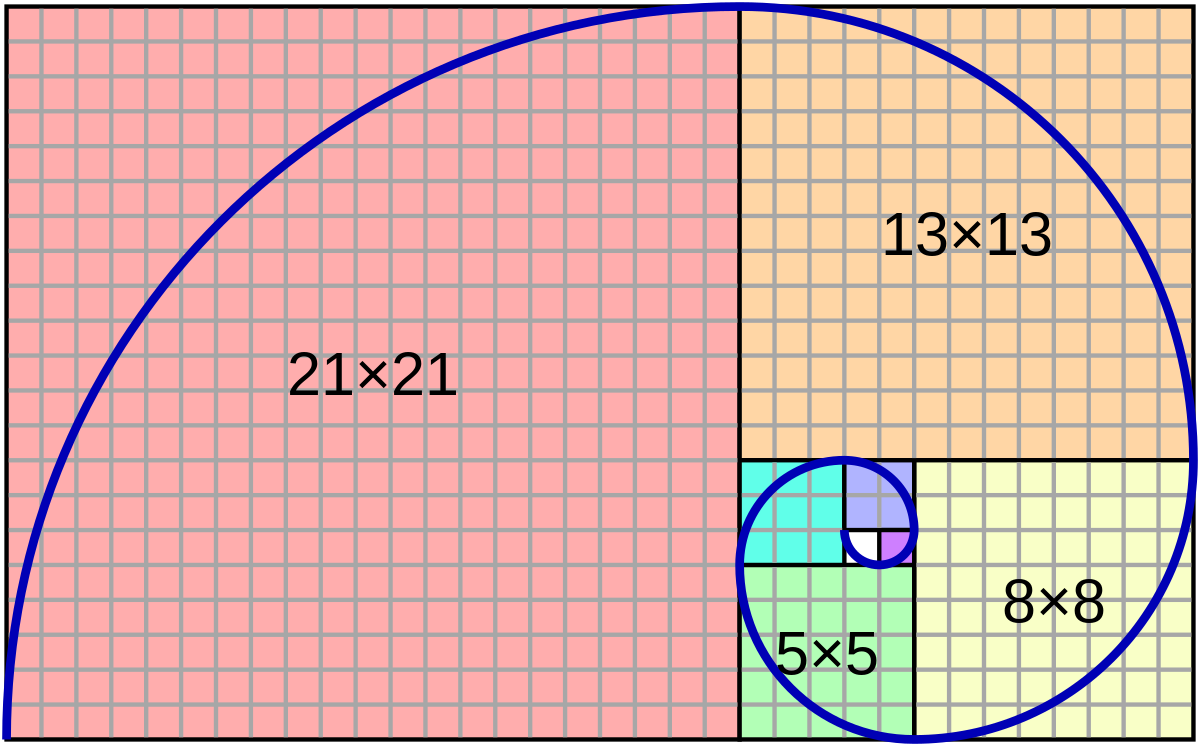
The numbers in the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…) have their own weird relationship with phi as well: as the Fibonacci numbers approach infinity, the ratio of two successive Fibonacci numbers will approach phi.
However, not all logarithmic spirals are Golden Spirals, something I looked up independently, which this book seemed to gloss over. So, while it’s true that “nature loves logarithmic spirals” and there are plenty of logarithmic spirals ranging in size from mollusk shells to spiral galaxies, not all of them are related to either phi or the Fibonacci sequence. However, many of the logarithmic spirals in plants are related to phi and the Fibonacci sequence. For example, pineapples usually have 5, 8, 13, or 21 spirals of increasing steepness on their surfaces, and all of these numbers are part of the Fibonacci sequence. Sunflower heads also display this pattern:
“Count the clockwise and counterclockwise spirals that reach the outer edge, and you'll usually find a pair of numbers from the sequence: 34 and 55, or 55 and 89, or—with very large sunflowers—89 and 144.” (From Science website).
Although this was not discussed in the book, the number of spirals on the head of Romanesco broccoli is also a Fibonacci number. Romanesco broccoli is also called “fractal broccoli” although it is only an approximate fractal.

(And no, this is not a messed-up product of genetic engineering; it’s been cultivated in Italy since the 1500’s.)
Speaking of fractals, phi shows up there as well. This isn’t surprising, since a fractal needs to be self-similar on different scales, and both the Golden Rectangle series of subdivisions and the Golden Spiral qualify. I had trouble with the Golden Sequence part but had a better time understanding the Golden Tree when it came to this chapter.
When I came to the last chapter, I learned that for some people, performing arithmetical calculations can trigger seizures. The condition is called epilepsia arithmetices, and fortunately it is very rare. For people with this condition, abnormal electrical activity is concentrated in the inferior parietal cortex, and damage to the same area also affects mathematical ability, writing, and spatial coordination.
And now I wish he would do a similar book for pi.
I'll admit it's not very catchy, but it will give you a far more accurate idea of what you're in for.


